2020-05-19 14:20:20 辽宁华图公考问答 http://ln.huatu.com/wenda/ 文章来源:辽宁华图
近三年的国考(2017年、2016年和2015年)和近两年的联考(2017年和2016年)中,都考到了数形结合的题目,而且多位于10道题或者15道题的后半部分,所以很多同学都选择直接放弃,一则没时间做,二则认为后面的题会越来越难,实际,这类题,只要掌握了正确的解题方法,在考场上是值得一做的题目。
针对这种题目我们采用的方法是“描点法””,即通过找题目中的几个特殊点进行验证,常找的特殊点有,极值点(极大值点或者极小值点)或者拐点等。那如何去验证,我们来看一道例题。
【例1】某学校组织学生春游,往返目的地时租用可乘坐10名乘客的面包车,每辆面包车往返的租金为250元。此外,每名学生的景点门票和午餐费用为40元,如要求尽可能少租车,则以下哪个图形最能反映平均每名学生的春游费用支出与参加人数之间的关系?
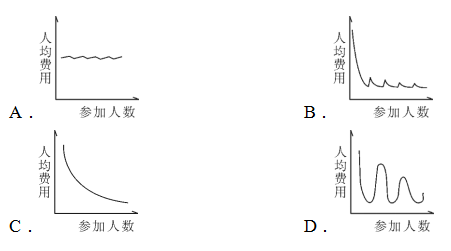
【华图点播】在这道题中大家应该首先能分析出,如果是1个人去春游的花费应该是最高的,相当于土豪包车,相当于极大值点:即当参加人数为1个人时,平均每名学生的春游费用支出为250+40=290元;随着人数逐渐增多,人均的费用会逐渐减小,当达到10人时,应该是最划算的时候是极小值点,即当参加人数为10个人时,平均每名学生的春游费用支出为65元;另外还需要找到一个拐点,当参加人数为11个人时,平均每名学生的春游费用支出接近90元;根据这几组数据对应选项中的曲线趋势。因此,选择B选项。
这道题就是非常典型的用描点法解决的数形结合的题目,不复杂,而且有章可循,易于掌握。
【例2】某集团三个分公司共同举行技能大赛,其中成绩靠前的X人获奖。如获奖人数最多的分公司获奖的人数为Y,问以下哪个图形能反映Y的上、下限分别与X的关系?
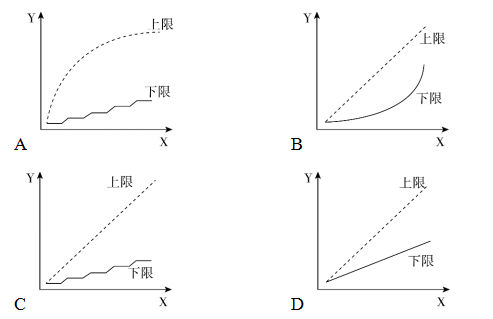
【华图点播】我们给X取值,来讨论Y的最大值和最小值,即上限和下限。当获奖人数x=1个人时,获奖人数最多的分公司获奖的人数y的上限为1,此时y的下限也为1,这个点并没有区分度;接下来再取值当获奖人数x=2个人时,获奖人数最多的分公司获奖的人数y的上限为2,即y=x,这是一条直线,故可以排除A选项,此时y的下限仍为1,即可出现其中两个分公司并列最多的情况,那么此时下限的值随着x值得增大,并没有发现变化,就会出现一条横线,故数形结合。因此,选择C选项。
通过这道题我们应该进一步意识到,这类题在考场上是值得一做的,不是难题,而且也是这两年出题人比较青睐的一种考法,将数学语言融入到图形中看似抽象,实则给我们提供了更多切入点。就像下面的例3,2017年的联考题,如果你树立了正确的解题思路,这道题是简单题。
【例3】某电信公司推出两种手机收费方式:A种方式是月租20元,B种方式是月租0元。一个月的本地网内通话时间t(分钟)与电话费S(元)的函数关系如图所示,当通话150分钟时,这两种方式的电话费相差?( )

A. 10元 B. 15元
C. 20元 D. 30元

【华图点播】观察图形可知,要知道两种收费方式的费用相差多少,实则就是让求途中三角形PQN的一条边长,如下图所示:由题意可得,三角形OMN相似于三角形PQN,根据相似三角形的基本性质,我们应该知道对应边成比例,我们只需求得这两个三角形的相似比,就了知道PQ是多少。由题可知N点到OM的横轴距离为100,到PQ的横轴距离为50,则PQ/MO=1/2,已知MO=20,则PQ=10,即两种方式的电话费相差10元。故正确答案为A。
对于这种图形结合的题目,就是个纸老虎,只要你找到了题目中的几个特殊点进行验证,常找的特殊点有,极值点(极大值点或者极小值点)或者拐点等,问题迎刃而解。
(编辑:辽宁华图07)

贴心微信客服

贴心QQ客服
上一篇:教师招聘备考,提高作文文采三步走